Welcome to one of the most active flamenco sites on the Internet. Guests can read most posts but if you want to participate click here to register.
This site is dedicated to the memory of Paco de Lucía, Ron Mitchell, Guy Williams, Linda Elvira, Philip John Lee, Craig Eros, Ben Woods, David Serva and Tom Blackshear who went ahead of us.
We receive 12,200 visitors a month from 200 countries and 1.7 million page impressions a year. To advertise on this site please contact us.
|

|
|
Tuning our guitars
|
You are logged in as Guest
|
|
Users viewing this topic: none
|
|
Login  | |
|

   
Andy Culpepper
Posts: 3028
Joined: Mar. 30 2009
From: NY, USA

|
 RE: Tuning our guitars (in reply to constructordeguitarras) RE: Tuning our guitars (in reply to constructordeguitarras)
|
|
|
I appreciate this guy's approach, but in practice, tuning is just not that exact of a science. Like you said, things start to drift as soon as you start playing, and if you're performing on a stage with hot lights, etc. then forget about it. All good guitarists will continually tune on the fly by ear during a performance, and some will even tune slightly differently depending on what key they're going to play in.
Personally I always tune my guitar the same way:
-first tune the A string using a tuner, fork, tone, whatever I have, then tune the rest of the guitar to that by ear.
-I tune the 6th string by matching the A at the 5th fret.
-Then the 4th string by fretting it at the second fret and matching it to an octave above the low E.
-Then the 3rd string by fretting it at the second fret and matching it to an octave above the A
-Then the 2nd string by fretting the 5th at the second fret, and matching the open B to that
-Then the 1st string by matching it to the open 6th.
This pretty much lets all the most common 1st position chords sound nicely in tune with the octaves in the right places. But every system of tuning is a bit of a compromise, between certain intervals, chords or open strings. Unless maybe you have one of those guitars with the weird squiggly frets, a perfectly intonated nut and saddle, tune every string down to the cent, etc. and even then you have issues...
_____________________________
Andy Culpepper, luthier
http://www.andyculpepper.com
|
|
|
|
REPORT THIS POST AS INAPPROPRIATE |
Date Feb. 9 2019 12:59:15
 |
|

   
jalalkun
Posts: 276
Joined: May 3 2017
From: Iraq, living in Cologne, Germany

|
 RE: Tuning our guitars (in reply to constructordeguitarras) RE: Tuning our guitars (in reply to constructordeguitarras)
|
|
|
never thought about spotlights getting it outta tune, but it makes sense 😂 can you show us this brochure, Ethan? 
i bring up the A string to 440, just like Andy, and then play the open E and A together to listen to the sympathetic vibrations the two strings create (dunno what else to call them), tune the E up until there are no vibrations and both sound clear. i do the same with the D string.
the G i sometimes tune on the 7th fret and compare with the D above, or on the 2nd and compare with the A string (again, just like Andy). the B either with open E string, E string 7th fret or compare B string 3rd fret with the D string. and the high E either with open E, open A or with the G string while pressing 3rd string on high E. then comes the fine tuning... all depends on the mood.
tuning with harmonics is also very nice, but I once had a weird guitar that I tuned with harmonics and one of the strings was suddenly a half step sharper than it needed to be when playing a chord. kind of odd.
_____________________________
My name is Jalal.
|
|
|
|
REPORT THIS POST AS INAPPROPRIATE |
Date Feb. 9 2019 16:18:29
 |
|

   
Ricardo
Posts: 15049
Joined: Dec. 14 2004
From: Washington DC

|
 RE: Tuning our guitars (in reply to Piwin) RE: Tuning our guitars (in reply to Piwin)
|
|
|
quote:
ORIGINAL: Piwin
Maybe that's why I sound awful 
Dumb question but won't all harmonics give you pure intervals?
Matching harmonics is simply a trick to get the strings to be tuned opened to one another, mainly you are matching the 4ths between two strings. THere will be arguements about how precise 4ths are supposed to be in the equal temp system, but in my experience having perfect 4ths between E-A, A-D,G-D, using the ear, results in a guitar in tune as good a possible without using a digital tuner. Comparing both I have always gotten green results.
G-B is a very dangerous string relation to try to match by ear, so I circumvent this by making sure the high E string is perfect 2 octave above low E, then making sure the B-E is a perfect 4th. Everytjme I check this against say 7th fret low E harm compared to open B it is always a perfect correlation. THerefore for it’s fine to tune the open B to the 7th fret of 6th from the get go. Also 7th fret harm of the 5th matches the open E string. Double check the two octave relation to both E’s to be sure, but it is always the same.
Always...unless your strings are going bad. Again if stings are going bad you have to rely on the open strings to be in tune relative to each other and make adjustments with your left hand technique. Normally the older and less true strings are, the more work you have to put in technique wise to play in tune. If all you do is throw a finger random into some fret position, that’s simply not pro IMO.
_____________________________
CD's and transcriptions available here:
www.ricardomarlow.com
|
|
|
|
REPORT THIS POST AS INAPPROPRIATE |
Date Feb. 11 2019 21:58:54
 |
|

   
kitarist
Posts: 1721
Joined: Dec. 4 2012

|
 RE: Tuning our guitars (in reply to Ricardo) RE: Tuning our guitars (in reply to Ricardo)
|
|
|
quote:
ORIGINAL: Ricardo
And guess what...when you fret a G at the third fret after having tuned your open G to the linear sum functioned “sharp by 2 cents” 4th interval sequence (implying an open G 6 cents sharp from what it should be based on low E), you end up with a perfectly tuned octave between the two G’s. Unless you fret the G carelessly like many do.
Now I am confused as to what that tuning method is. I thought it was as follows:
1. Tuning fork A -> tune open A (5th string) to that (5th fret harmonics, which is 2 octaves up from open A, which is unison with the tuning fork, which is 440Hz);
2. Tune 6th string 5th fret harmonics to match 5th string 7th fret harmonics. This results in 6th string being 2 cents sharper than what it should be.
3. Tune 4th string 7th fret harmonics to match 5th string 5th fret harmonics. This results in 4th string being 2 cents flatter than what it should be.
4. Tune 3rd string 7th fret harmonics to match 4th string 5th fret harmonics. This results in 3rd string being 2 cents flatter than what it should be based on 4th string, which is also 2 cents flatter than what it should be based on the properly tuned open A - so it is 4 cents flatter than what 3rd string should be.
Hmm, not sure how the rest goes for string 2; let's say
5. Maybe you tune string 1 open E to low E 5th fret harmonics. This results in string 1 being 2 cents sharper than it should be (same as string 6).
6. Tune 2nd string 5th fret harmonics to match 1st string 7th fret harmonics. This results in 2nd string being 2 cents sharper than what it should be based on the 1st string, so 4 cents sharper than it should be.
So compared to equal temperament EADGBE tuning, we have:
E+2, A=true, D-2, G-4, B+4, E+2
For the G-g octave example, if you mean 3rd fret G on string 6 and open g on string 3, that open G would be 6 cents flat compared to the 3rd fret G on string 6.
Man I am starting to doubt all this, it is late. Someone let me know if I effed up in deriving this.
_____________________________
Konstantin
|
|
|
|
REPORT THIS POST AS INAPPROPRIATE |
Date Feb. 12 2019 5:43:33
 |
|

  
Piwin
Posts: 3566
Joined: Feb. 9 2016

|
 RE: Tuning our guitars (in reply to Ricardo) RE: Tuning our guitars (in reply to Ricardo)
|
|
|
Damn. I'm having one of those "duh" moments 
I'd never even considered the possibility of making the string go flat at the same fret...
Now I'm actually sort of pissed that after quite a few years studying with various flamenco teachers, not one ever bothered to bring up something that, now that you say it, just seems so obvious.
Anyways, thanks, I'm going to have to start exploring this.
quote:
if you mean 3rd fret G on string 6 and open g on string 3, that open G would be 6 cents flat compared to the 3rd fret G on string 6
Shouldn't it be -2 cents and not -6? 2 + (-4)?
If I'm following this correctly, then "Unless you fret the G carelessly like many do." is the important part. That theoretical gap of 2 cents (or 6 if I miscalculated and you had it right) is in practice closed by proper positioning of your finger on the 6th string 3rd fret. I haven't explored this yet, but I imagine it means that to get an exact octave between those 2 notes then the proper position on the 6th string would have to be leaning away from the bridge. You'd still be off by -4 cents from the open A string since that's the one you tuned as true, but your two Gs would be in unison.
_____________________________
"Anything you do can be fixed. What you cannot fix is the perfection of a blank page. What you cannot fix is that pristine, unsullied whiteness of a screen or a page with nothing on it—because there’s nothing there to fix."
|
|
|
|
REPORT THIS POST AS INAPPROPRIATE |
Date Feb. 12 2019 14:08:39
 |
|

   
kitarist
Posts: 1721
Joined: Dec. 4 2012

|
 RE: Tuning our guitars (in reply to Piwin) RE: Tuning our guitars (in reply to Piwin)
|
|
|
quote:
ORIGINAL: Piwin
quote:
if you mean 3rd fret G on string 6 and open g on string 3, that open G would be 6 cents flat compared to the 3rd fret G on string 6
Shouldn't it be -2 cents and not -6? 2 + (-4)?
If we have E+2, A=true, D-2, G-4... then the low G in 6th string 3rd fret is also 2 cents sharp (as its open string is). Compared to THAT sharpened G, the 4th string open G octave interval is 6 cents flat (in other words, even if the 3rd string open G was true, it would still be 2 cents flat compared to the sharpened low G; so it is 6 cents total difference from the sharpened G).
BTW I always fine-tune further so certain areas of the fretboard (maybe where I would play the piece mostly) sound ok. My guitar is not great. For example I find that if open G is exactly true, the 9th fret E (same pitch as open string high E, so easy to compare) is always a bit sharp. So I flatten open G a bit. And if your guitar has multiple intonation issues in different positions, that could overwhelm any adjustments one can make for tuning open strings. It is too bad that we can't just tune all the frets, not just the nut.
Ricardo is right that you can modulate fretted pitch by the amount of pressure and pull/push with your left hand. In fact some classical guitar books refer to it as an advanced tool to subtly sharpen/flatten notes with your left-hand pressure/pull if needed to compensate for out of tune note.
EDIT: I meant to include a visual reference for greater clarity but got distracted. Here it is:
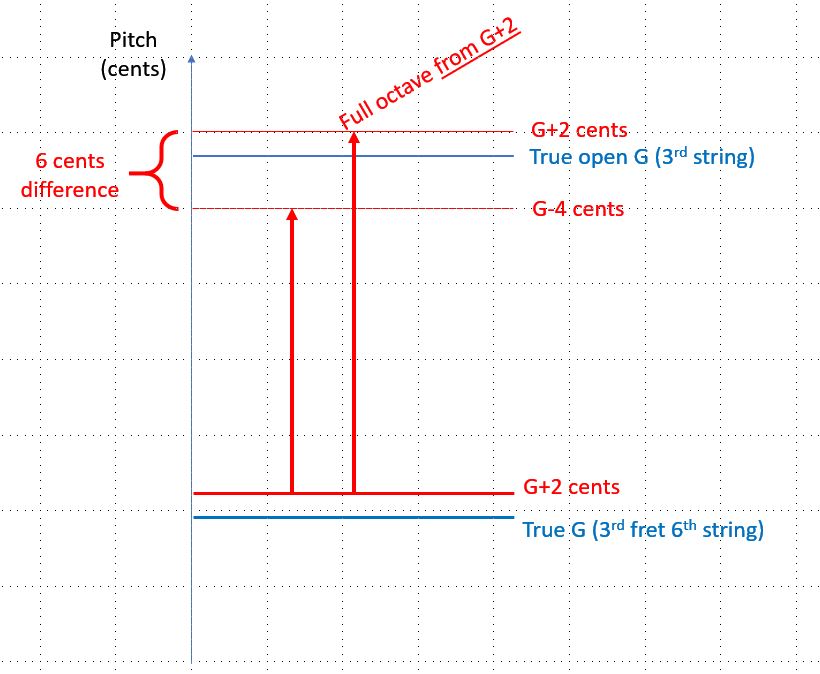
Images are resized automatically to a maximum width of 800px
 Attachment (1) Attachment (1)
_____________________________
Konstantin
|
|
|
|
REPORT THIS POST AS INAPPROPRIATE |
Date Feb. 12 2019 17:11:19
 |
|
 New Messages New Messages |
 No New Messages No New Messages |
 Hot Topic w/ New Messages Hot Topic w/ New Messages |
 Hot Topic w/o New Messages Hot Topic w/o New Messages |
 Locked w/ New Messages Locked w/ New Messages |
 Locked w/o New Messages Locked w/o New Messages |
|
 Post New Thread
Post New Thread
 Reply to Message
Reply to Message
 Post New Poll
Post New Poll
 Submit Vote
Submit Vote
 Delete My Own Post
Delete My Own Post
 Delete My Own Thread
Delete My Own Thread
 Rate Posts
Rate Posts
|
|
|
Forum Software powered by ASP Playground Advanced Edition 2.0.5
Copyright © 2000 - 2003 ASPPlayground.NET |
0.078125 secs.
|


 Printable Version
Printable Version















 Guess I'll have to start paying attention to that more.
Guess I'll have to start paying attention to that more. 

 New Messages
New Messages No New Messages
No New Messages Hot Topic w/ New Messages
Hot Topic w/ New Messages Hot Topic w/o New Messages
Hot Topic w/o New Messages Locked w/ New Messages
Locked w/ New Messages Locked w/o New Messages
Locked w/o New Messages Post New Thread
Post New Thread